Chapter 7.
Green Thumb Row
Row analysis, interval inventory, chord inventory
The following tone row is used in many of the examples in this discourse. Sometimes it is useful to do an analysis of your tone-row before you begin to compose with it. Other times, I prefer to just use the row freely and discover its characteristics as I am writing. For the sake of a more comprehensive understanding I have provided an analysis below.
‘Green Thumb Row’
A C# Bb D F F# B C D# G E G#

Interval inventory
The above row illustrates a variation on a symmetrical series. Strictly speaking this violates the definition of a symmetrical row because the row when played backwards isn’t an exact mirror. If the intervals are accepted in their smallest form, for example we convert all 7ths to 2nds, 6ths to 3rds etc. then we do have a symmetrical row. Similarly, for our intents and purposes, and for ease of analysis, when we do an intervallic inventory, it is unnecessary to individually account for the inversions of intervals. So, again minor 6ths will be considered the same as major 3rds.
With regards to intervallic inventory we notice the following intervals present:
m2-2 occurances
m3-4 occurances
M3-4 occurances
P4-1 occurances
m3-4 occurances
M3-4 occurances
P4-1 occurances
I would consider this row to have a moderate amount of intervals to work with. There are no tri-tones, no major seconds and a somewhat heavier representation of thirds.
Chordal inventory
I picked up this method of chordal inventorying from my first guitar teacher Jody Rech. We started by outlining the chords present in a major scale, and then a minor scale. By learning music theory in this basic way, I was able to easily figure out the ‘feel’ of a chord progression. For example the impetus of a dominant 7 chord leading to a tonic, or the feel of a deceptive cadence. We applied this taking of chord inventory to pentatonic scales, whole-tones scales, octatonic scales etc. It didn’t take long for me to extend this idea to all pitch sequences.
It seems an easy way to notice all potential tonal implications within a given row. When we do this however we will be accepting our tone rows in their gestalt. In other words, we won’t require the pitches to be adjacent to each other in order to build a chord, but instead will set different parameters more conducive to the TONL compositional method.
It should be noted that for this method to work, we have to convert our row into a scale. In this way we are ‘de-serialising’ our row, this won’t work if we don’t use the prime interval set.
First we will split the row into two hexachords, and then put these pitches into prime order (smallest interval order). The first hexachord has two possibilities:

A Bb C# D F Gb

C# D F F# A Bb
Both prime sets span a major 6th. Now that both of these are in prime order we can do our chord inventory. It doesn’t matter which one we use, we will get the same results.

Major chords:
D, Bb, F#
D, Bb, F#
 Minor chords:
Minor chords: D-, Bb-, F#-

Augmented chords:
F+, Bb+, Db+
F+, Bb+, Db+
The above chords require some enharmonic spelling changes.
We will do the same with the second hexachord. Our two options here also span a major 6th.

G Ab B C D# E

B C D# E G Ab

Major chords:
C, Ab, E
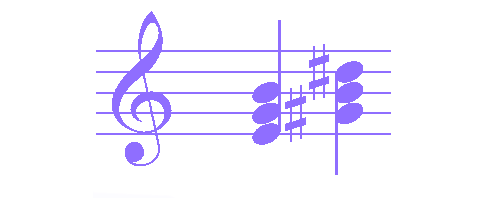
Minor chords:
E-, G#-
E-, G#-
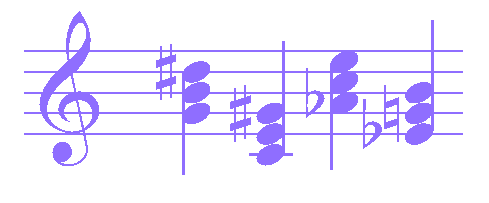
Augmented chords:
G+, C+, Ab+, Eb+
G+, C+, Ab+, Eb+
Essentially what we are trying to do is derive chordal material from a tone row that, if used in a serial fashion, has little or no chordal options. Green Thumb Row does have two triads present (Bb major in the first hexachord, C minor in the second hexachord) but the notes that come immediately before and after these triads both contradict any kind of Bb tonality.
It would be remiss of me if I didn’t address that this triadic inventory certainly doesn’t have to stop here. We could do this inventory through all chord extensions. For the sake of brevity I have done an inventory of 7th chord possibilities using the second hexachord below.
Major seventh chords: E Maj7, C Maj7,
Minor major seventh chords: Emin/maj7, G#min/maj7
Augmented major seventh: C Aug/maj7
Minor major seventh chords: Emin/maj7, G#min/maj7
Augmented major seventh: C Aug/maj7