Chapter 1.
TONL Composition Introduction
Twelve-tone Organic Non-Linear Composition
—
A new method of composing with twelve tones which are related with one another
Why TONL? The T of TONL is probably the most self explanatory of the bunch, and it stands for twelve tone. I wanted to make mention that for the intents and purposes of introducing this method I have restricted the musical examples to using the 12 pitches of the chromatic scale. Certainly, exploration into microtonal idioms as well as other non-western pitch organisation systems warrant further examination.

Blind Texas Marlin
When I first heard the description of music developing Organically, I was playing with a band called Blind Texas Marlin. The melodica player used this word to describe how the music developed from one section to another with out any preordained instructions. It was a way to differentiate between purely improvisatory music and that which is structured, but contains improvisatory elements. When we would play together we would know that we were starting at point A and moving to point B but the way that we would get there was never the same. TONL uses this same concept in its compositional process.
Non-Linear refers to the freedom with which we treat our tone-row. This could also be described as deserialising the music.
The following treatise will contain many disclaimers. I’d like to make clear what TONL is as well as what it is not. For one, I am not reinventing the wheel. I am not writing a dissertation on how to compose. This is simply a new look and approach to an old idea. A background in composition would be helpful in understanding many of the concepts put forth, but isn’t strictly necessary.
Throughout, enharmonic spellings of notes are observed to make for easier visual recognition. As such, intervals such as diminished 4ths, augmented 5ths, diminished octaves etc. will be avoided.
Because TONL is primarily concerned with harmony, I have purposefully limited the variables of texture, timbre, dynamics, and rhythm so as to more easily focus our attention on the content at hand. Obviously these elements will play a huge part in how our music is perceived and written and cannot be overlooked in the larger scheme of things.
Many of the examples used in the explanation of TONL are written on two staves, and played on piano. These examples needn’t be thought of as music for piano, but rather as sketches that could bear further development and be adapted for any instrumentation. A few of the examples have been arranged for piano trio to show how a fuller ensemble might soud playing some of these passages.
As you can see with the orchestrations some liberty has been taken with the sketch from which the orchestration is borne. Choosing to adhere strictly to the sketched material would have hindered the piece’s realisation and so some freedom was taken in this regard. As mentioned earlier the most important facet is to serve the music and not strictly follow a method that helps us get there. We use TONL when needed and discard it when it no longer serves us.
Chapter 2.
Background
How the TONL method came to be
Serialism has occupied a corner of my mind ever since hearing Glenn Gould’s 1968 recording of Schoenberg’s Five Pieces For Piano Op. 23. I was about 5 years old, my mother was cooking dinner in the kitchen, and my dad and I were listening to some records he had recently purchased at our local Dog Ear Record Store. Among the collection were Guru Guru’s UFO, Stockhausen’s Gruppen, and this Schoenberg recording of solo piano music. I remember the huge, heavy, brown headphones that my dad put on my head and how he cued up the second track on the A-side. That opening movement’s music seemed to come from another planet. The way it unfolded and exposed these musical ideas turned something on in my head. Until that point, music just sort of passed me by. I didn’t really take notice of sounds.
![]()
Apart from this, I can remember consistently getting a part of a song stuck in my head, and then my brain would hold on to this little excerpt, turn it around and play with it like a musical version of a spatial awareness test. I would experiment mentally with moving the musical tidbit around rhythmically, imparting different accents to it, and generally just messing it up, until eventually I couldn’t remember where I had even started. All of this happened before I had any idea how to write or read musical notation, or had begun playing an instrument.
The music that I was introduced to on this Glenn Gould record led to other early serial works such as Webern’s String Trio Op. 20, and String Quartet Op. 28, and the music of Milton Babbitt. Admittedly this kind of music has become an obsession of mine more than once.
It wasn’t until around age 15 that I had a composition teacher who encouraged me to explore composing using this serial method. Coming from a background of jazz and improvisation, the strict rules of serialism were hard to get used to at first. I liked the idea of putting limitations on certain compositional material while keeping the freedom in other aspects, and had done just that in many other musical settings but never in the same way that serialism imposes on the music. We didn’t just serialise pitch sequences, but rhythm, dynamics, and articulation as well. Our class had a rather peculiar core of musicians (piano, guitar, trumpet, saxophone, violin, clarinet) in it that we could write for and so I set about writing my first compositions exploring the possibilities of this new method.
At this point in my life I hadn’t yet begun to play cello. I had no experience of being in the ‘classical’ music world and had no classical music training (whatever this is meant to mean). It was my first encounter with musicians who didn’t come from a background of creating music themselves, but rather a background where they were trying to accurately translate the notes on a page into sounds. When we would rehearse I would refer to harmonic sequences and chords in a piece that seemed very obviously to be structural markers, but these students didn’t hear the music in the same way. For them, (and as I have discovered over the years, many musicians) music theory is a separate entity of music, something that one could easily ignore and because they put their fingers in the right places, the right sounds come out of the instruments.
At this time I also discovered that my musical upbringing which consisted of Schoenberg, Monk, Sun Ra, Varese, Zappa, Takemitsu, Metallica, Slayer, was not the norm. I had heard Mozart, Beethoven, and Bach but I didn’t share the reverence for them that my classmates did. For me music was and is about creating something new. At that young age what I heard when I listened to these classical masters was antique, ancient. It wasn’t until I developed a love for history that I went back and took a closer look at their music. A subconscious decision that brought about its own set of musical obsessions.
I also quickly discovered that not only my classmates, but also some of my music teachers really hated serial music and the composers who wrote this music, so I suppressed my need to write in this way and followed the other student’s leads. It was much easier to get performances, and audiences seemed to like my music more. It is from these beginnings that my foundation and approach to writing music took shape.
No matter how much I tried to repress the desire to write this way, the desire just kept getting stronger. I had to find sneaky ways to incorporate these sounds into my compositions and little by little this combination of traditional harmony and serial music became part of my musical vocabulary.
For me, music written using serial grammar takes on an entirely different kind of enjoyment when you play it. The first extended tonality piece that I can recall playing is Pierrot Lunaire. While this isn’t serial music, it was my first free-atonal experience as a performing instrumentalist. I had the incredible opportunity to play Pierrot during my undergraduate studies at Illinois State University under the direction of Glenn Block. When other schools and venues heard that we were performing Pierrot, they also programmed the piece, and since I had already been performing the piece for a few months I was the go-to ‘Pierrot’ cellist for hire. This carried on for about 6 months and culminated with a series of concerts held at Eastern Illinois University directed by Peter Hestermann. The concept of his concerts was to pair music of the early 1900’s with horror films of the same time period. Hestermann’s idea was that these movies would have been so much better served had they used music of these early avant-garde composers instead of the boring, pedestrian stock music that was used on the original soundtracks.
Upon entering university I was met with an onslaught of different musical viewpoints. The major trends in academia at that time were minimalism and the music of the New Complexity. There was also a huge contingency of composers who embraced the abstract graphic notations of Earle Brown and John Cage. While these kinds of music interested me very intensely for varying periods of time nothing seemed to have the staying power that the early serialists held in my mind. But alas, serialism found its way into antiquity as well. Berg’s Lyric Suite is nearly 100 years old; the freshness that his harmonies once brought to the world are now looked at as things to be studied in a classroom, rarely heard in concert.

Chapter 3.
Serial Music Brief
For the newcomer to the 12-tone method
The 12-tone method was a way of composition developed in Europe, namely Austria, in the 1920’s. There are varying opinions on how this method came about, but it is generally believed that some combination of the natural progression of traditionally tonal music and the academic fervour of trying to create something new, led to what is now termed atonality. Many composers didn’t like this newly coined term because of its negative implications. It was presumed by many critics that atonality was actually ‘anti-tonality.’ Further confusion came about when theorists said this term couldn’t be applied to mediaeval music and music of the renaissance, both of which often didn’t have this supposed tonal centre.
Eventually, a systematisation of this atonality came to light, hence serialism. Without getting too in depth as to what makes serialism different from other methods of composition I pose a few of the main facets; pitches are put into an order that is dictated by a tone row. By making this tone row we eliminate a few key elements of traditional tonality such as preferential treatment of certain pitches, tendency tones, and the magnetic push and pull of harmonic progression that comes with chords and having a dominant/tonic relationship.
To avoid ambiguity I will only use the word atonal to refer to music without an obvious tonal centre. However, occassionally I will refer to passages as being ‘more atonal’ or ‘less atonal.’
Chapter 4.
The Row
Brindle’s Categorisations
Most 12-tone composition books emphasise a few points to consider when composing a tone row. For the sake of completion and comprehensive understanding I’ll summarise very briefly what Brindle has written in Serial Composition (p. 4-17) regarding distinguishing different types of tone rows.
Melodic Series
The first two types of rows that he describes he titles ‘melodic series,’ and ‘tonal series.’ He uses the former distinction to indicate a row that has an ‘expressive melodic arc.’ I think a fair comparison of the ‘melodic series,’ can be made to George Pearle’s ‘pitch-cell’ compositions. These row’s intervallic choices function almost like leitmotifs throughout the composition.
Berg’s Lyric Suite
![]()

Brindle’s distinction between the first two types of series is indeed miniscule. He writes that in much of the music of Berg and Dallapiccola ‘...it is obvious that on many occasions the melodic character of the series has been a prime consideration.’ Later he goes on to describe the above tone-row indicating that Berg’s intention was to use a series ‘...with strong lyrical possibilities.’ How this differs from the following ‘tonal series’ is not made clear. He does however go on to highlight how certain rows (ex. Dallapiccola’s Il Prigioniero ‘Hope series’ and ‘Liberty series’) were written to express and represent certain emotions and are used by the composer to do just that.
Tonal Series
The second type of row Bridle describes is the ‘tonal series.’ These rows exemplify elements of tonality, perhaps pitch sequences that outline or imply certain chords, or utilise tonicising cadential figures. Rows that utilise whole-tone and octatonic patterns are also included in this section.
Secondary tone-row from Benjamin Frankel’s Curse of the Werewolf
![]()

Frankel uses this row to build tension before an attack. The sequential triads retain the serialised nature of the music while their juxtaposition of unrelated keys works well to build suspense in various scenes.
One frequently cited piece that uses a strong ‘tonal series,’ is Berg’s Violin Concerto (1935).
Berg’s Violin Concerto
He advertently constructed the tone row out of major and minor triads, which could easily lead to melodic monotony. Intervallically, he only has these intervals to work with:
M2, m3, M3
To avoid this potential for monotony he treats the row with considerable freedom.
You’ll also notice that unlike the Frankel set which utilises triads that are rather distantly related, Berg constructed his set using triads that are very closely related. Throughout the piece he is careful to avoid feelings of dominant to tonic relationships that could be easily exposed if the row were played in retrograde.
Atonal Series
The next row category is the ‘Atonal Series.’ Without going into too much detail here, the ‘atonal series’ is constructed in such a way as to avoid any tonal implications. For example, no triads or chord implications, groups of wholetone relationships, consecutive 4ths/5ths, and no successive note groupings that could imply a chromatic chord (ex. diminished seventh chord).
Permissible three note cluster in the ‘atonal series.’





Naturally these three note clusters could (with the exception of #1 and #3) fit into a key. The main point is that they are not triadic in nature and don’t imply any singular key. This lack of implication is important to their function within a row.
Webern was quite fond of this type of row and used it in many compositions to great effect. One such example is from his Variations for Piano Op. 27.
Variations for Piano Op. 27.

Variations for Piano not only exploits this ‘atonal series’ but also shows great examples of symmetry within the piece. In this particular example, Webern effectively eliminates any of the tonal directions in music and introduces us to a truly unique and new sounding vocabulary.
It needs to be mentioned that using an ‘atonal series’ doesn’t necessarily beget an atonal sounding result. Similarly, using a ‘tonal series’ doesn’t necessarily produce a tonal sounding result.
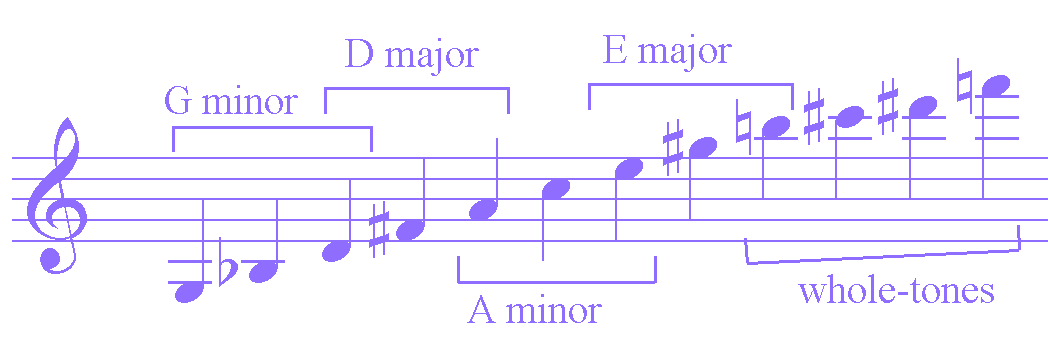
Below is the row used in Lou Harrison’s Symphony in G:
Symphony in G
![]()

Take notice that if we look at the notes in groups of threes, few traditionally harmonic triads are readily apparent. There is an outlined A major chord in pitches 9, 10, 11, and we can extend this to include pitch 8, a D, which extends this harmony to be a D major 7 chord. With these as the exception the other three note groupings that could imply a key, when combined with a fourth note from the row (from either side of the group) are immediately disavowed of this notion. To be sure, this isn’t 100% an ‘atonal series,’ but one worth mentioning and listening to because it illustrates a very clear difference compared with the examples of the ‘tonal series’ above.
Harrison achieves rather tonal sounds with his permutations of this tone-row by using many different forms of the row as well as by starting on pitches in the middle of the row so as to suit his desired harmonic impetus. In relatively short compositions he would often use upwards of 10 row forms, a strategy that certainly bears further examination.
I consider the ‘atonal series’ to be far more delicate than the ‘tonal series.’ If we stray too far from the atonal series or treat it with too much freedom then its innate characteristics are lost, it ceases to be an atonal series. Whereas the tonal series can be treated with considerable freedom, and can essentially still maintain its core traits.
A very generalised statement could be made as such:
The more a row resembles a ‘tonal series,’ the freer we need to treat it. The more a row resembles an ‘atonal series,’ the less free we should treat it.
The more a row resembles a ‘tonal series,’ the freer we need to treat it. The more a row resembles an ‘atonal series,’ the less free we should treat it.
Symmetrical Series
This brings us to the ‘symmetrical series.’ Brindle uses this term to indicate rows that have portions which are symmetrical in their interval structure. The simplest example would be to show one point of symmetry in the middle of the row.
Ex. D E Eb C# F C | F# B G A Bb Ab
This row could be described as an intervallic palindrome of sorts. The first interval is a major second followed by a minor second. If we look at the row starting at the end and work backwards we also get the same pattern.
All-Interval Series and Symmetrical All-Interval Series
Brindle goes on to describe two more related series types, ‘all-interval series’ and ‘symmetrical all-interval series.’ The names are rather self explanatory and won’t be discussed in depth here, however we will look at two examples for the sake of completion
The ‘all-interval series,’ as the name suggests, contains all possible intervals. This isn’t as special as it sounds as what this really is, is the five smallest intervals with their inversions. A more interesting characteristic of the ‘all-interval series’ is that it must contain two tri-tones, one in the middle and one between the first and last note of the series.
A composer who is always mentioned in the same breath as the ‘all-interval series’ is that of Fritz Heinrich Klien. Klein’s Die Maschine Op. 1︎︎︎ shows to wonderful effect how this ‘all-interval series’ can be used. He creates provocative musical characters that belie any inclination of a tone-row while simultaneously remaining quite faithful to it.
Short Series and Long Series
The final row type that Brindle introduces, he calls ‘short series’ and ‘long series.’ These row types are tone rows that are shorter or longer than 12-tones. The rows that are shorter have some notes purposely avoided. The rows that are longer essentially add notes to the end of the series for the purpose of increasing intervallic material. Obviously, the longer rows will require a note occurring more than once in the series and therefore placing a slight emphasis on its importance. These rows with respect to TONL will be addressed in the next chapter.
Short Series and Long Series
Composing using a serialised method with a tone row that doesn’t use all of the 12 pitches is nothing new or ground breaking. A few great examples of this can be heard in Ruth Crawford Seeger’s Diaphonic Suite No. 1 and her String Quartet 1931. Stravinsky’s Septet also gives us an insight into how we can work with the serial method while using fewer than 12 tones. So how would this work in tandem with TONL? We can approach this the same way that we did the rows of 12 pitches, but we need to be aware that with fewer pitches present it becomes much easier to get magnetically drawn to a key. This being said, it is all the more important to create a row that has few or if possible zero resemblance to a traditionally tonal construct.
For example:
D F C# D# G A G#
The potential for interesting material derived from the set above is plentiful. Also, when we move into more diatonically based material it will contrast nicely and rather easily create different characters between the two.

If we take the viewpoint from the opposite extreme, we can create a tone row whereby all of the pitches when considered in their gestalt would make up a defined key.
For example a potential 7 note row could be:
B F# G# D C# A E
Although the row doesn’t leave us with much in the way of sounding like anything other than A major and its modal counterparts it does let us take a different perspective on TONL’s overall approach. Where previously we started with a 12-tone row and found different ways to move away from it towards varying tonal centres, here we can find ways to move toward a more chromatic vocabulary. By introducing contradictory tones and avoiding tonicising gestures interesting results can still be achieved.

The above passage sounds rather like a pandiatonic composition similar to material that one might encounter in the music of Milhaud, or Copland.
In the next step I took my original row of 7 notes (which were purposely selected to fit within the key of A major) and introduced 2 more pitches (C natural and G natural). The passage below demonstrates this method, which really still sounds rather tonal to the ear. I tried to maintain the contour and texture of the original piece while intuitively changing certain notes to accommodate for our two new pitches added to our row. We should notice that I didn’t re-write the row to include C and G, but rather kept my original row, and simply altered the previously composed material. The results would be quite different if I ‘inserted’ the new pitches into the original 7-tone row instead of ‘tweaking’ the pandiatonic material from above.

I continued again in the same fashion as the previous passage this time adding two more notes (F natural and D#). The same intuitive approach was followed and the result is now a passage of material that teeters on the edge of aurally identifiable key centres. We could examine this passage as we have previous ones and discover how these small additions and alterations to the pitches affect the impetus of the music, but really the most important thing to note is how the music sounds. As we gradually add these chromatic pitches to what would be A major, the strength of the diatonic interval relationships weaken, and the pitches begin to take on an importance of their own. This is largely what TONL helps to explore. TONL is at once a systematisation of pitches while also being a method by which we can move away from this systematic organisation and discover new ways of approaching harmony, melody, and composition in general.

I composed another example that does something similar to the above method with one added caveat. This piece strictly follows the serialisation of the following tone-row:
C# B E A G F# D
Obviously this row fits into D major or B minor. Extra care has to be taken so that we don’t inadvertently begin to sound like either of these keys. With a bit of practise, you’ll be able to avoid the magnetism that the corresponding major and minor keys possess.
The excerpt below shows another example utilising this same method, this time written for piano trio.

EXCERPT 2
