Berg’s Lyric Suite

Tonal Series

The second type of row Bridle describes is the ‘tonal series.’ These rows exemplify elements of tonality, perhaps pitch sequences that outline or imply certain chords, or utilise tonicising cadential figures.  Rows that utilise whole-tone and octatonic patterns are also included in this section.

Secondary tone-row from Benjamin Frankel’s Curse of the Werewolf

Frankel uses this row to build tension before an attack.  The sequential triads retain the serialised nature of the music while their juxtaposition of unrelated keys works well to build suspense in various scenes.

One frequently cited piece that uses a strong ‘tonal series,’ is Berg’s Violin Concerto (1935).

Berg’s Violin Concerto

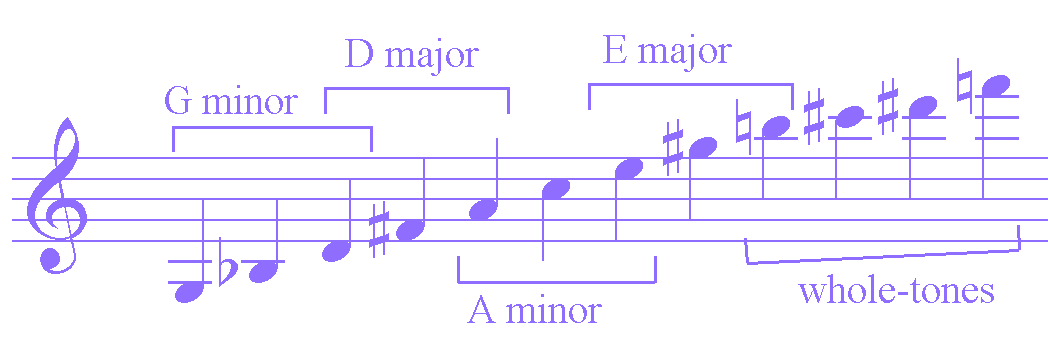
He advertently constructed the tone row out of major and minor triads, which could easily lead to melodic monotony.  Intervallically, he only has these intervals to work with:

To avoid this potential for monotony he treats the row with considerable freedom.

You’ll also notice that unlike the Frankel set which utilises triads that are rather distantly related, Berg constructed his set using triads that are very closely related.  Throughout the piece he is careful to avoid feelings of dominant to tonic relationships that could be easily exposed if the row were played in retrograde.

Atonal Series
The next row category is the ‘Atonal Series.’  Without going into too much detail here, the ‘atonal series’ is constructed in such a way as to avoid any tonal implications.  For example, no triads or chord implications, groups of wholetone relationships, consecutive 4ths/5ths, and no successive note groupings that could imply a chromatic chord (ex. diminished seventh chord).

Permissible three note cluster in the ‘atonal series.’

Naturally these three note clusters could (with the exception of #1 and #3) fit into a key.  The main point is that they are not triadic in nature and don’t imply any singular key.  This lack of implication is important to their function within a row.

Webern was quite fond of this type of row and used it in many compositions to great effect.  One such example is from his Variations for Piano Op. 27.

Variations for Piano Op. 27.

Variations for Piano not only exploits this ‘atonal series’ but also shows great examples of symmetry within the piece.  In this particular example, Webern effectively eliminates any of the tonal directions in music and introduces us to a truly unique and new sounding vocabulary.

It needs to be mentioned that using an ‘atonal series’ doesn’t necessarily beget an atonal sounding result.  Similarly, using a ‘tonal series’ doesn’t necessarily produce a tonal sounding result.

Below is the row used in Lou Harrison’s Symphony in G:

Symphony in G

Take notice that if we look at the notes in groups of threes, few traditionally harmonic triads are readily apparent. There is an outlined A major chord in pitches 9, 10, 11, and we can extend this to include pitch 8, a D, which extends this harmony to be a D major 7 chord. With these as the exception the other three note groupings that could imply a key, when combined with a fourth note from the row (from either side of the group) are immediately disavowed of this notion. To be sure, this isn’t 100% an ‘atonal series,’ but one worth mentioning and listening to because it illustrates a very clear difference compared with the examples of the ‘tonal series’ above. 

Harrison achieves rather tonal sounds with his permutations of this tone-row by using many different forms of the row as well as by starting on pitches in the middle of the row so as to suit his desired harmonic impetus.  In relatively short compositions he would often use upwards of 10 row forms, a strategy that certainly bears further examination. 

I consider the ‘atonal series’ to be far more delicate than the ‘tonal series.’  If we stray too far from the atonal series or treat it with too much freedom then its innate characteristics are lost, it ceases to be an atonal series.  Whereas the tonal series can be treated with considerable freedom, and can essentially still maintain its core traits. 

A very generalised statement could be made as such:

The more a row resembles a ‘tonal series,’ the freer we need to treat it.  The more a row resembles an ‘atonal series,’ the less free we should treat it.

Symmetrical Series
This brings us to the ‘symmetrical series.’  Brindle uses this term to indicate rows that have portions which are symmetrical in their interval structure.  The simplest example would be to show one point of symmetry in the middle of the row.

This row could be described as an intervallic palindrome of sorts.  The first interval is a major second followed by a minor second.  If we look at the row starting at the end and work backwards we also get the same pattern.


All-Interval Series and Symmetrical All-Interval Series
Brindle goes on to describe two more related series types, ‘all-interval series’ and ‘symmetrical all-interval series.’  The names are rather self explanatory and won’t be discussed in depth here, however we will look at two examples for the sake of completion  

The ‘all-interval series,’ as the name suggests, contains all possible intervals.  This isn’t as special as it sounds as what this really is, is the five smallest intervals with their inversions.  A more interesting characteristic of the ‘all-interval series’ is that it must contain two tri-tones, one in the middle and one between the first and last note of the series. 

A composer who is always mentioned in the same breath as the ‘all-interval series’ is that of Fritz Heinrich Klien. Klein’s Die Maschine Op. 1︎︎︎ shows to wonderful effect how this ‘all-interval series’ can be used.  He creates provocative musical characters that belie any inclination of a tone-row while simultaneously remaining quite faithful to it.


Short Series and Long Series
The final row type that Brindle introduces, he calls ‘short series’ and ‘long series.’  These row types are tone rows that are shorter or longer than 12-tones.  The rows that are shorter have some notes purposely avoided.  The rows that are longer essentially add notes to the end of the series for the purpose of increasing intervallic material.  Obviously, the longer rows will require a note occurring more than once in the series and therefore placing a slight emphasis on its importance.  These rows with respect to TONL will be addressed in the next chapter.